Problem
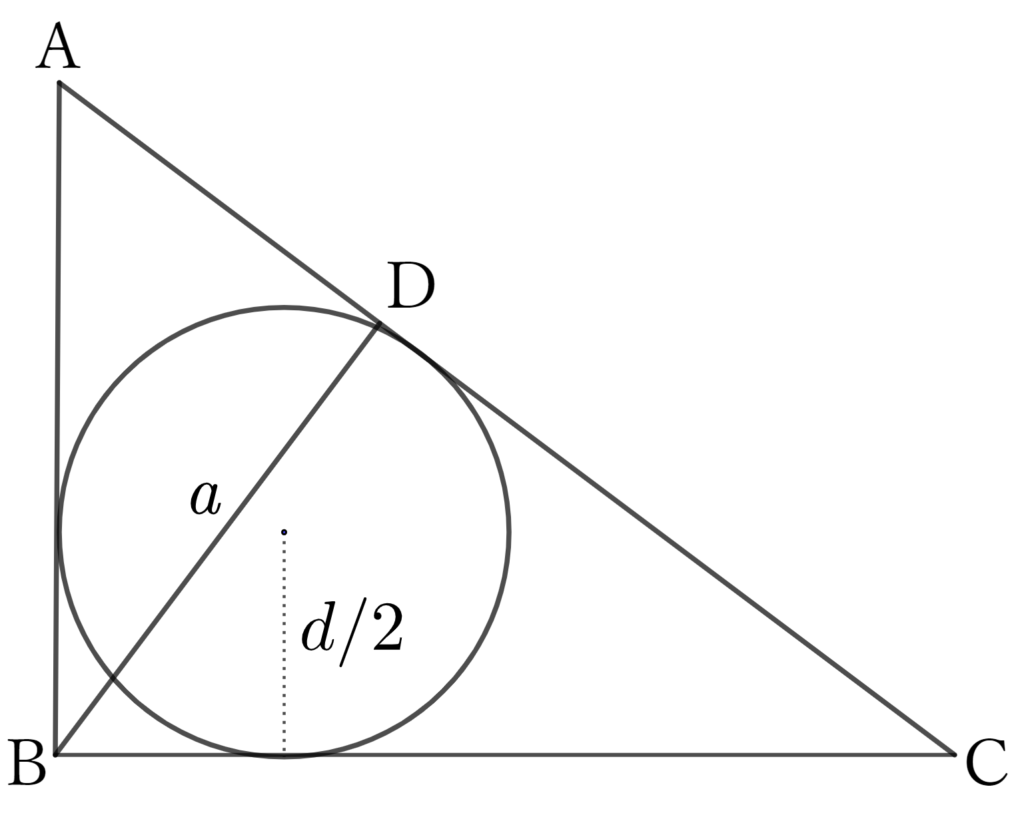
If the diameter of the circle inscribed in the three sides of a right-angled triangle $ABC$ is $d$, and the length of the perpendicular $BD$ from the right angle $∠B$ to the hypotenuse $CA$ is known to be $a$, What are the lengths of the short side $AB$, the long side $BC$, and the hypotenuse $CA$?
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
The area $S$ of the right triangle $ABC$ above can be expressed in two ways. First, it follows that
$$S=\frac{1}{2}×AB×BC,$$
$$∴ 2S=AB×BC. —– [1]$$
Next, we see that
$$S=\frac{1}{2}×CA×a,$$
$$∴ 2S=a×CA. —– [2]$$
Therefore, we have
$$AB×BC=a×CA. —– [3]$$
From the figure, we see that
$$AB+BC=CA+d, —–[4]$$
$$(AB+BC)^2=(CA+d)^2,$$
$$AB^2+BC^2=CA^2+(2d×CA-2AB×BC+d^2),$$
$$∴ 2d×CA-2AB×BC+d^2=0. —–[5]$$
$(∵ AB^2+BC^2=CA^2.)$
Substituting $[3]$ into $[5]$ gives
$$2d×CA-2a×CA+d^2=0,$$
$$2a×CA-2d×CA=d^2,$$
$$∴ CA=\frac{d^2}{2a-2d}. —– [6]$$
Substituting [6] into [4], we get
$$AB+BC=\frac{2ad-d^2}{2a-2d}. —– [7]$$
When we square $AB-BC$, we get
$$\begin{eqnarray}&&(AB-BC)^2=AB^2+BC^2-2AB×BC\\[5pt]&=&CA^2-2a×CA\\&=&CA×(CA-2a)\\&=&\frac{d^2}{2a-2d}×\frac{d^2-4a^2+4ad}{2a-2d}\\&=&\frac{d^4+4ad^3-4a^2d^2}{(2a-2d)^2},\end{eqnarray}$$
$$∴ AB-BC=-\frac{\sqrt{d^4+4ad^3-4a^2×d^2 }}{2a-2d}. —– [8]$$
From $[7]+[8]$, it follows that
$$2AB=\frac{2ad-d^2-d\sqrt{d^2+4ad-4a^2}}{2a-2d},$$
$$∴ AB=\frac{d×(2a-d-\sqrt{d^2+4ad-4a^2})}{4a-4d}.$$
From [7]-[8], we have
$$2BC=\frac{2ad-d^2+d\sqrt{d^2+4ad-4a^2}}{2a-2d},$$
$$∴ BC=\frac{d×(2a-d+\sqrt{d^2+4ad-4a^2})}{4a-4d}.$$
$$ $$
$$ $$
$$ $$
$$Ans.\quad CA=\frac{d^2}{2a-2d},$$
$$AB=\frac{d×(2a-d-\sqrt{d^2+4ad-4a^2})}{4a-4d},$$
$$BC=\frac{d×(2a-d+\sqrt{d^2+4ad-4a^2})}{4a-4d}.$$
Reference
Yoshikazu Yamakawa, ed. (1997) Okayama ken no Sangaku (Sangaku in Okayama Prefecture), p.51; pp.307-308.