Problem
The point $P$ on the bisector of $∠BAC$ is equidistant from its two sides $AB$ and $AC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
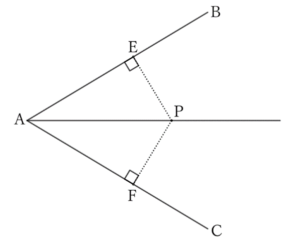
Drop a perpendicular line from the point $P$ to $AB$ and $AC$, and let the feet be $E$ and $F$ respectively.
For two right triangles $⊿APE$ and $⊿APF$, they share the side $AP$, and
$$∠EAP=∠FAP,$$
$$∠PEA=∠PFA (=∠R),$$
$$∴ \ ⊿APE≡⊿APF.$$
$$∴ \ PE=PF.$$
That is, the point $P$ is equidistant from $AB$ and $AC$.
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.6