Problem
If the two sides $AB$ and $AC$ of $∠BAC$ are, respectively, parallel to the two sides $DE$ and $DF$ of $∠EDF$, then the bisector $AM$ of the former angle and the bisector $DN$ of the latter are parallel or perpendicular to each other.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
(1) Assume that $AB$ and $DE$, and $AC$ and $DF$ are, respectively, parallel in the same direction.
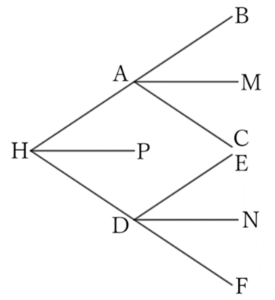
The extension lines of $FD$ and $BA$ always intersect, and let their intersection point be $H$, and the bisector of $∠AHD$ be $HP$.
At this time, since $FH$ and $CA$ are parallel,
$$∠BAC=∠AHD,$$
$$∴ \ ∠BAM=∠AHP,$$
$$∴ \ AM∥HP.$$
Similarly, since $BH$ and $ED$ are parallel,
$$∠EDF=∠AHD,$$
$$∴ \ ∠FDN=∠DHP,$$
$$∴ \ DN∥HP,$$
$$∴ \ AM∥DN.$$
(2) Suppose that only one pair of $AB$ and $DE$ or $AC$ and $DF$ is parallel in opposite directions.
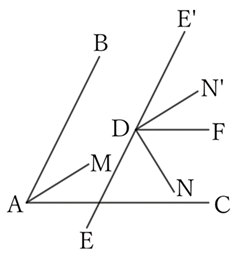
Since $∠E’DF$ is a complementary angle of $∠EDF$, the two sides $BA$ and $AC$ of $∠BAC$ and the two sides $E’D$ and $DF$ of $∠E’DF$ are, respectively, parallel in the same direction.
Thus, the bisector $DN’$ of $∠E’DF$ is parallel to $AM$.
However, the bisector $DN$ of $∠EDF$ and $DN’$ are perpendicular.
Therefore, $DN$ is perpendicular to $AM$, which is parallel to $DN’$.
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.8-9