Problem
Two triangles, in which the three corresponding sides are equal respectively, are congruent.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
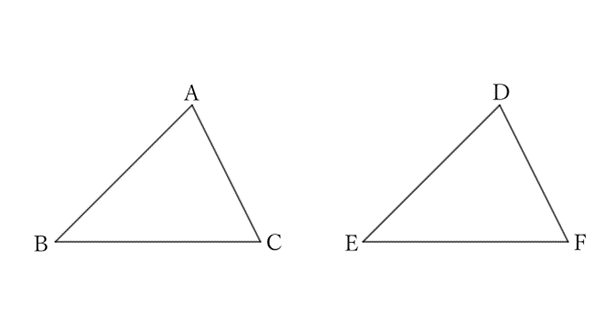
In $△ABC$ and $△DEF$,
$$AB=DE, \quad BC=EF \quad and \quad AC=DF.$$
As shown in the figure below, place $E$ on top of $B$, $F$ on top of $C$, and $D$ on top of $D’$ (on the opposite side of $A$ from $EF$).
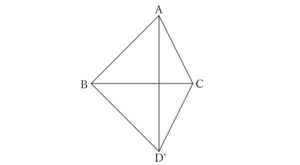
Then,
$$AB=D’B,$$
$$∴ \ ∠BAD’=∠BD’A.$$
$$AC=D’C,$$
$$∴ \ ∠CAD’=CD’A.$$
$$∴ \ ∠BAD’+∠CAD’=∠BD’A+CD’A.$$
That is,
$$∠BAC=∠BD’C=∠EDF,$$
$$∴ \ AB=DE, \quad AC=DF \quad and \quad ∠A=∠D.$$
$$∴ \ △ABC≡△DEF.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.9-10