Problem
Two right triangles which have equal hypotenuses and the other equal sides respectively are congruent.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
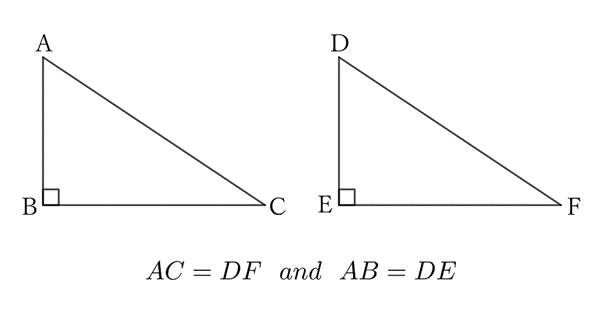
Suppose that $AC=DF$ and $AB=DE$ in $⊿ABC$ and $⊿DEF$ where $B$ and $E$ are right angles.
When $D$ and $E$ overlaps $A$ and $B$ repsectively, $EF$ overlaps $BC$ because $∠ABC=∠DEF=∠R$.
Then, since $AC=DF$, $F$ overlaps $C$. Thus,
$$BC=EF.$$
$∴ \ ⊿ABC≡⊿DEF.$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.10