Problem

---

$$ $$

$$ $$

$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

---

Solution

For $△ABC$ and $△A’B’C’$, suppose that

$$BC=B’C’, \quad AD=A’D’ \quad and \quad ∠BAC=∠B’A’C’.$$

Then, place $B’$ on top of $B$, $C’$ on top of $C$, and put $A$ and $A’$ on the same side of $BC$.

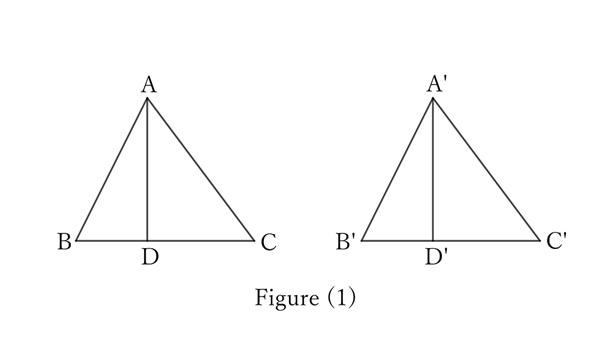
As shown in Figure (1), if $A$ and $A’$ overlap,

$$△ABC≡△A’B’C’.$$

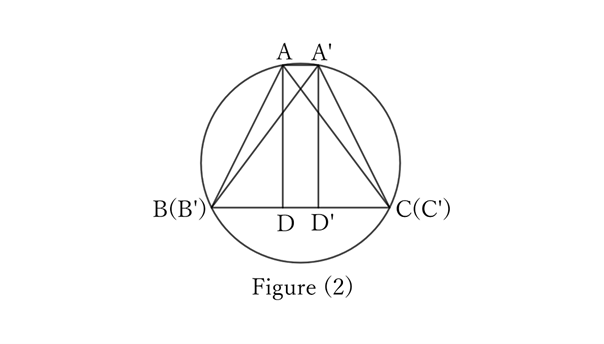
As shown in Figure (2), if $A$ and $A’$ do not overlap, then $AA’∥BC$ is clear because $AD=A’D’$ and $∠A=∠A’$.

Thus, $B, C, A$ and $A’$ are on the same circumference (circumferential angle theorem).

$$AB=A’C’,$$

$$AC=A’B’.$$

$$∴ \ △ABC≡△A’B’C’.$$

In both cases, the two triangles are congruent.

---

Reference

Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2^nd edition), Seikyo-Shinsha, p.10