Problem
When the two sides of one of two triangles are equal to the two sides of the other, and the angles to one set of equal sides are also equal, the angles to the other set of equal sides are equal or supplementary angles. In the former case, the two triangles are congruent.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
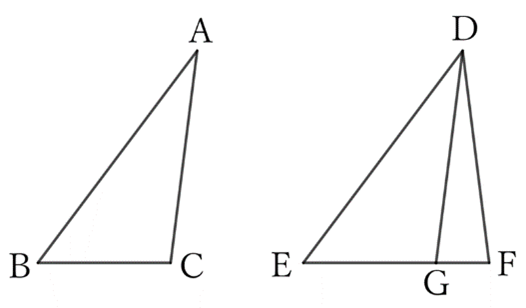
Suppose that $AB=DE, \ AC=DF$ and $∠B=∠E$ in $△ABC$ and $△DEF$.
If we place $△ABC$ on top of $△DEF$, $A$ on $D$, $AB$ on $DE$, and $C$ on the same side of $DE$ as $F$, then $B$ overlaps $E$, and $BC$ comes above $EF$.
When $C$ overlaps $F$,
$$△ABC≡△DEF,$$
$$∴ \ ∠C=∠F.$$
If $C$ does not overlap $F$ and comes to $G$ on $EF$, then
$$DG (=AC)=DF,$$
$$∴ \ ∠F=∠DGF.$$
$$∴ ∠ACB=∠DGE=180°-∠F.$$
That is, in this case, $∠C$ and $∠F$ form supplementary angles to each other.
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.10-11