Problem
Regarding two congruent triangles $△ABC$ and $△A’B’C’$, when the two pairs of sides $AB$ and $A’B’$ and $AC$ and $A’C’$ are perpendicular to each other, the remaining pair $BC$ and $B’C’$ are also perpendicular to each other. However, assume that $∠A$ and $∠A’$ are not right angles.

$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
Let the intersections of $AB$ and $A’B’$, $AC$ and $A’C’$, and $BC$ and $B’C’$ be $D, E$, and $F$, respectively.
By assumption,
$$AB⊥A’B’ \qquad and \qquad AC⊥A’C’,$$
$$∴ \ ∠ADC’=∠R \qquad and \qquad ∠AEB’=∠R.$$
Also, since $△ABC≡△A’B’C’$,
$$∠C=∠C’.$$
Therefore, regarding the quadrilateral $CDC’F$, $∠DCF$ and $∠DC’F$ should be supplementary angles to each other, and $∠CDC’$ and $∠CFC’$ should also be supplementary angles to each other.
Thus,
$$∠CFC’=2∠R-∠CDC’=2∠R-∠R=∠R.$$
$$∴ \ BC⊥B’C’.$$
$$ $$
$$ $$
$$ $$
Note
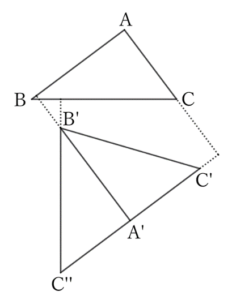
Suppose that $∠A=∠A’=∠R$. Then if we create $△A’B’C^”$ congruent to $△A’B’C’$ as shown in the figure,
$$BC⊥B’C^”.$$
However, $BC$ and $B’C’$ may not be orthogonal.
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.11