Problem
When two sides of one triangle are equal to two sides of another triangle, and the angles between the two sides are unequal, the side facing the larger angle is greater than the side facing the smaller angle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
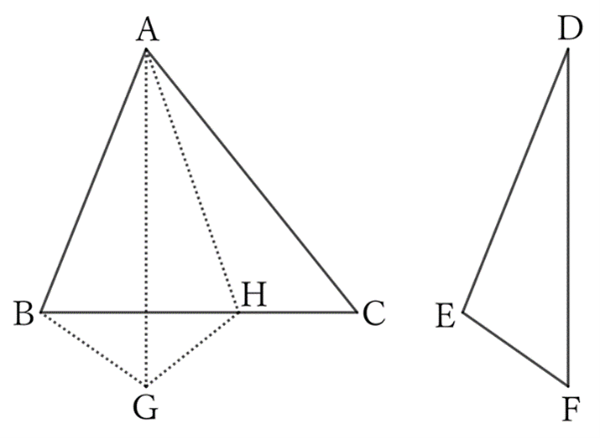
Regarding $△ABC$ and $△DEF$, let $AB=DE, \ AC=DF,$ and $∠BAC>∠EDF$.
If we place $D$ on top of $A$, $E$ on top of $B$, and the two triangles are on the same side of $AB$, and $F$ comes to the position of $G$, then
$$∠EDF<∠BAC,$$
$$∴ \ ∠BAG<∠BAC.$$
Therefore, $AG$ is within $∠BAC$.
When we draw the bisector $AH$ of $∠GAC$, $△GAH$ and $△CAH$ have the same two sides and their equal included angles.
Thus,
$$△GAH≡△CAH,$$
$$∴ \ HG=HC.$$
Regarding $△BHG$,
$$BH+HG>BG.$$
Since $BC=BH+HC$,
$$BC=BH+HG>BG.$$
Since $BG=EF$,
$$BC>EF.$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.12