Problem
The sum of two sides of a triangle is greater than the third side, and the difference between the two sides is less than the third side.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
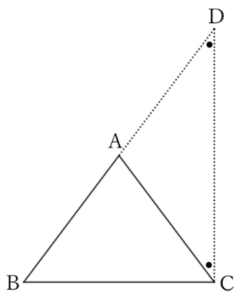
If we extend $BA$ to $D$, set $AD=AC$, and connect $D$ and $C$, we get
$$∠D=∠ACD,$$
$$∴ \ ∠DCB>∠D,$$
$$∴ \ BD>BC,$$
$$∴ \ AB+AC>BC.$$
Therefore, the sum of the two sides is greater than the third side.
From this, we also get
$$AB>|BC-AC|.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.12