Problem
In $△ABC$, when $AC$ is larger than $AB$, $AD$ connecting any $D$ on $BC$ and $A$ is smaller than $AC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
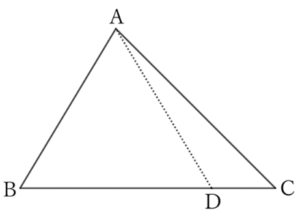
If $AC>AB$, then from the problem $0038$,
$$∠B>∠C.$$
Since $∠ADC$ is an exterior angle of $△ABD$,
$$∠ADC>∠B,$$
$$∴ \ ∠ADC>∠C,$$
$$∴ \ AC>AD.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.12