Problem
If we take any points $D, \ E$, and $F$ on sides $BC, \ CA$, and $AB$ of $△ABC$, we get
$$3(AD+BE+CF)<5(AB+BC+CA).$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
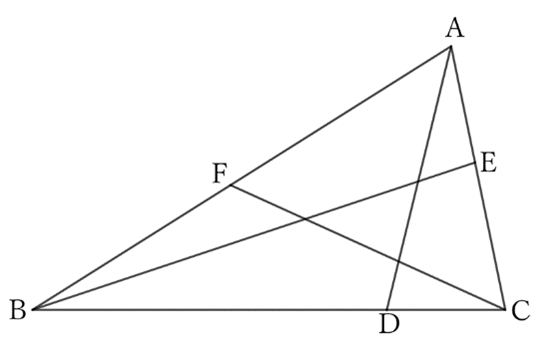
If $AB$ is the maximum side of $△ABC$ and $CA$ is the minimum side, then according to the problem $0043$,
$$AD<AB, \quad BE<AB\quad and \quad CF<BC.$$
$$∴\ AD+BE+CF<2AB+BC$$
$$∴ \ 3(AD+BE+CF)<6AB+3BC. \qquad [1]$$
From the problem $0042$,
$$AB<BC+CA.$$
Therefore,
$$AB<2BC+5CA. \qquad[2]$$
From $[1]$ and $[2]$,
$$3(AD+BE+CF)+AB<6AB+3BC+2BC+5CA,$$
$$∴ \ 3(AD+BE+CF)<5(AB+BC+CA).$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.13