Problem
In $△ABC$, when $BC<AC<AB$, take any point $P$ in the triangle, create line segments $AP$, $BP$, and $CP$, and let $M$ be the intersection of $BC$ and the extension of $AP$, then,
$$(1) \ AM+BC<AB+AC.$$
$$(2) \ AP+BP+CP<AB+AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
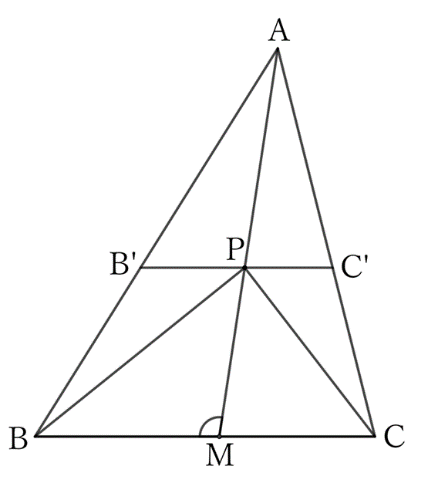
$(1)$ Since $∠AMB$ is the exterior angle of $△AMC$,
$$∠AMB>∠C.$$
However, depending on the conditions,
$$AC<AB,$$
$$∴ \ ∠C>∠B,$$
$$∴ \ ∠AMB>∠B,$$
$$∴ \ AM<AB. \qquad [1]$$
Depending on the conditions,
$$BC<AC. \qquad [2]$$
From $[1]$ and $[2]$,
$$AM+BC<AB+AC.$$
(2) Draw a straight line through $P$ parallel to $BC$, and let the intersections of $AB$ and $AC$ be $B’$ and $C’$, respectively.
From the proof of $(1)$,
$$AP+B’C'<AB’+AC’. \qquad [3]$$
Also, regarding $△BPB’$,
$$BP<B’P+B’B. \qquad [4]$$
Regarding $△CPC’$,
$$CP<C’P+C’C. \qquad [5]$$
From $[3]$~$[5]$,
$$AP+B’C’+BP+CP<AB’+AC’+B’P+B’B+C’P+C’C,$$
$$AP+B’C’+BP+CP<(AB’+B’B)+(AC’+C’C)+(B’P+C’P),$$
$$∴ \ AP+BP+CP<AB+AC.$$
$$(∵ \ AB’+B’B=AB, \quad AC’+C’C=AC, \quad and \qquad B’P+C’P=B’C’)$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.13-14