Problem
In the obtuse triangle $ABC$, let $∠C$ be the obtuse angle.
Suppose that
$$BD=\frac{1}{2} (AB+AC), \qquad and \qquad DE∥BC.$$
Take any point $F$ inside $△ADE$ or on $DE$, draw a straight line through $F$ and parallel to $AB$, and let $G$ be the point of intersection with $BC$.
If we take $H$ and $I$ on the side $BC$ so that $HG=GI$,
$$FH+FI>AB+AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
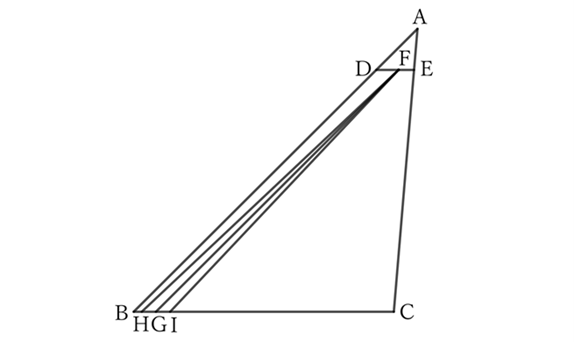
When $F$ is on $DE$,
$$FG=BD=\frac{1}{2} (AB+AC),$$
$$∴ \ 2FG=AB+AC.$$
Regarding $△FHI$, since $HG=GI$, from the property of the median line,
$$FH+FI>2FG,$$
$$∴ \ FH+FI>AB+AC.$$
When $F$ is inside $△ADE$,
$$FH+FI>2FG>2BD,$$
$$∴ \ FH+FI>AB+AC.$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.14