Problem
If we take any point $F$ inside $△ABC$ and any two points $H$ and $I$ on $BC$, will the proposition $AB+AC>FH+FI$ always hold?
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
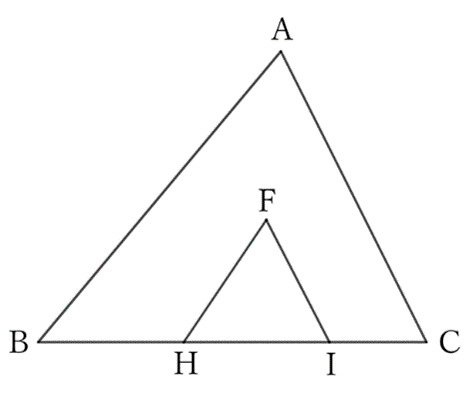
If we take $F, \ H$ and $I$ as in the previous question $0049$,
$$FH+FI>AB+AC.$$
Therefore, it is not always possible to say that $AB+AC>FH+FI$.
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.14