Problem
The sum of the interior angles of a triangle is equal to two right angles, and the exterior angle is equal to the sum of its inner opposite angles.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
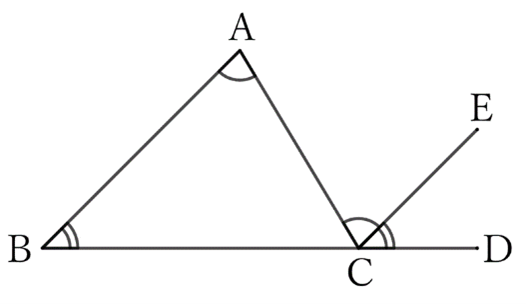
Draw a straight line $CE$ passing through the point $C$ of $△ABC$ and parallel to $AB$.
Since $AB∥CE, \ ∠A$ and $∠ACE$ are alternate angles, and $∠B$ and $∠ECD$ are the corresponding angles, from the problem $0016$,
$$∠A=∠ACE \quad and \quad ∠B=∠ECD,$$
$$∴ \ ∠A+∠B=∠ACE+∠ECD,$$
$$∴ \ ∠A+∠B=∠ACD. \qquad [*]$$
If we add $∠ACB$ to both sides of $[*]$, we have
$$∠A+∠B+∠ACB=∠ACD+∠ACB=2∠R,$$
Since $∠ACB$ is $∠C$ of $△ABC$,
$$∠A+∠B+∠C=2∠R.$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.14