Problem
When extending any side of a triangle, its exterior angle is greater than any of its inner opposite angles.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
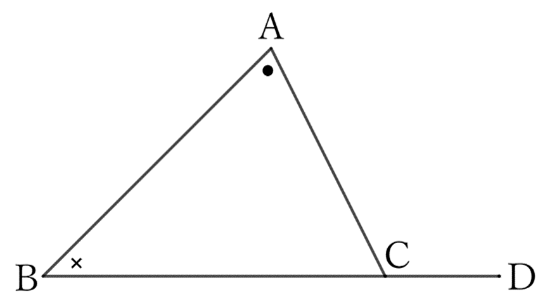
From the previous question $0053$, $$∠A+∠B+∠C=2∠R.$$ However, $$∠C+∠ACD=2∠R,$$ $$∴ \ ∠ACD=∠A+∠B.$$ Therefore, the exterior angle $∠ACD$ of $△ABC$ is greater than both the inner opposite angles $∠A$ and $∠B$.
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.14-15