Problem
In $△ABC$ where $AB>AC$, if we take $AD$ equal to $AC$ on $AB$, we have
$$∠ADC=\frac{1}{2} (∠B+∠C) \quad and\quad ∠BCD=\frac{1}{2} (∠C-∠B)$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
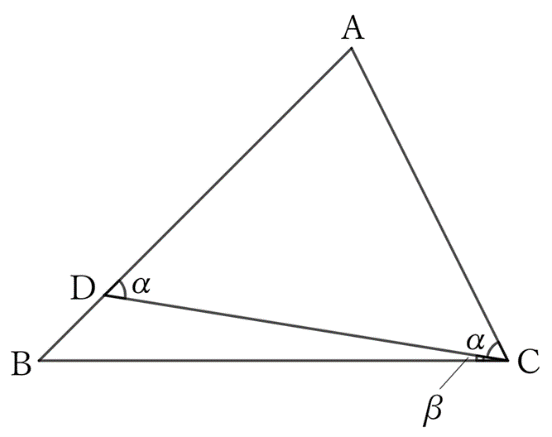
If $∠ADC=∠ACD$ and these angles are $α$ and the angle of $∠BCD$ is $β$, then
$$∠B=α-β \qquad and \qquad ∠C=α+β,$$
$$∴ \ \frac{1}{2} (∠B+∠C)=α,$$
$$∴ \ ∠ADC=\frac{1}{2}(∠B+∠C).$$
Similarly,
$$\frac{1}{2} (∠C-∠B)=β,$$
$$∴ \ ∠BCD=\frac{1}{2} (∠C-∠B).$$
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.15