Problem
Let $D$ be the foot of the perpendicular drawn from the vertex $A$ to the opposite side $BC$ of $△ABC$, and let $E$ and $F$ be the midpoints of the sides $BC$ and $AB$, respectively. Then $$∠DFE=|∠B-∠C|$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
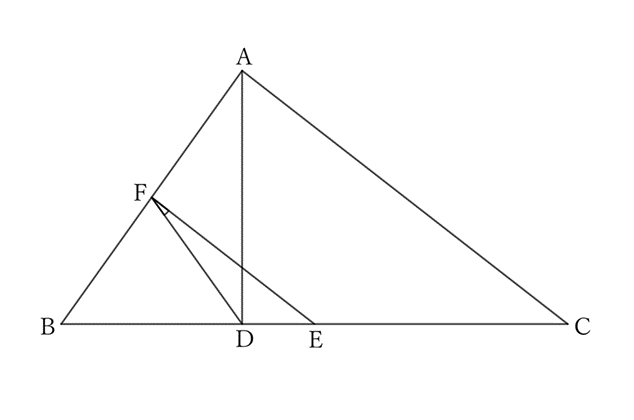
As shown in the figure, if $∠B>∠C$,
$$FB=FD,$$
$$∴ \ ∠B=∠FDB.$$
$$∠FDB=∠DFE+∠FED,$$
$$∴ \ ∠B=∠DFE+∠BEF.$$
Since $△ABC〜△FBE$,
$$∠BEF=∠C,$$
$$∴ \ ∠B=∠DFE+∠C,$$
$$∴ \ ∠DFE=∠B-∠C.$$
If $∠B<∠C$, thinking similarly, we have
$$∠DFE=∠C-∠B.$$
When $∠B=∠C$,
$△ABC$ becomes an isosceles triangle with $A$ as the vertex. Therefore, $D$ and $E$ overlap, and
$$∠DFE=∠B-∠C=0.$$
In any case,
$$∠DFE=|∠B-∠C|.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.15