Problem
The sum of the lengths of perpendiculars drawn from the three vertices of a triangle to their opposite sides is less than the sum of the lengths of the three sides of the triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
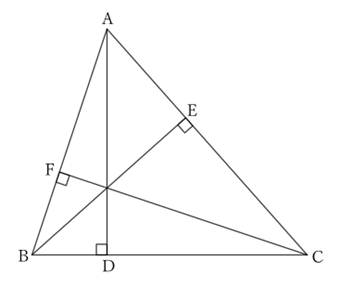
As shown in the figure, regarding the right triangle $ABD$, $$AD<AB.$$ Regarding the right triangle $BCE$, $$BE<BC.$$ Regarding the right triangle $CAF$, $$CF<CA.$$ Therefore, $$AD+BE+CF<AB+BC+CA.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.16