Problem
In $△ABC$, suppose $AC>AB$, and if we draw the perpendicular $AD$ from $A$ to $BC$, we have
$$∠DAC>∠DAB \qquad and \qquad DC>DB$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
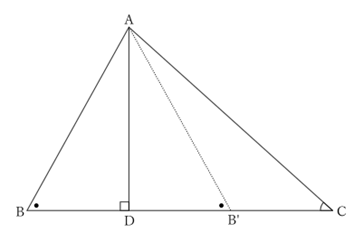
Since $AD⊥BC$, $∠DAB$ and $∠DAC$ are complementary angles of $∠B$ and $∠C$, respectively.
Since $AB<AC$,
$$∠B>∠C,$$
$$∴ \ ∠DAC>∠DAB.$$
Then, if we take $∠DAB’$, which is equal to $∠DAB$, inside $∠DAC$, $B’$ is on $DC$ and $BD=DB’$. Thus,
$$DC>DB’,$$
$$∴ \ DC>DB.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.16