Problem
The bisector $AE$ of the apex angle $∠A$ of a triangle $ABC$ lies between the median line $AM$ and the perpendicular $AD$ drawn from this apex angle to the opposite side.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
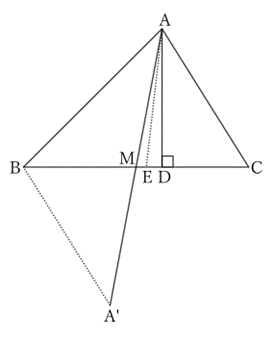
Let $AB>AC$.
If we take a point $A’$ on the extension of $AM$ such that $AM=MA’$,
$$AM=A’M, \qquad MC=MB \quad and \qquad ∠AMC=∠A’ MB,$$
$$∴ \ △AMC≡△A’ MB,$$
$$∴ \ AC=A’ B \qquad and \qquad ∠CAM=∠BA’ M,$$
$$∴ \ AB>A’ B, \qquad (∵ \ AB>AC)$$
$$∴ \ ∠BA’ M>∠BAM,$$
$$∴ \ ∠CAM>∠BAM.$$
Therefore, the bisector $AE$ of $∠A$ lies between $AM$ and $AC$.
However,
$$∠B<∠C, \qquad (∵ AB>AC)$$
$$∴ \ ∠BAD>∠DAC.$$
Therefore, $AE$ is between $AD$ and $AB$.
Thus, $AE$ is between $AM$ and $AD$.
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.16