Problem
If the feet of the perpendicular lines drawn from the two vertices $B$ and $C$ of a triangle $ABC$ to the opposite sides $AC$ and $AB$ are $E$ and $F$, respectively, then the straight line connecting the midpoint of the line segment $EF$ and the midpoint of the side $BC$ is perpendicular to $EF$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
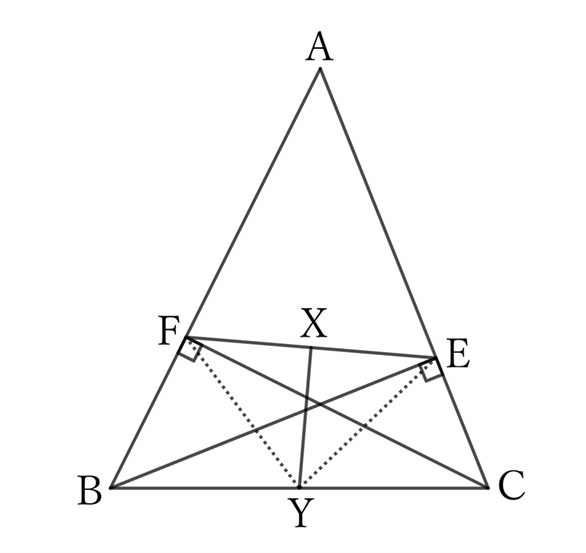
Let the midpoints of $EF$ and $BC$ be $X$ and $Y$, respectively. At this time, since $Y$ is the midpoint of the hypotenuse $CB$ of the right triangle $BEC$,
$$BY=YE.$$
Similarly, since $Y$ is the midpoint of the hypotenuse $CB$ of the right triangle $BFC$,
$$BY=YF,$$
$$∴ \ YE=YF.$$
Therefore, the triangle $YEF$ is an isosceles triangle with $Y$ as its vertex, and $X$ is the midpoint of its base $EF$.
$$∴ \ YX⊥EF.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.16-17