Problem
Suppose that any straight line passes through the vertex $A$ of a triangle $ABC$. The feet $D$ and $E$ of the perpendicular lines drawn from $B$ and $C$ to the above line are equidistant from the midpoint $M$ of the side $BC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
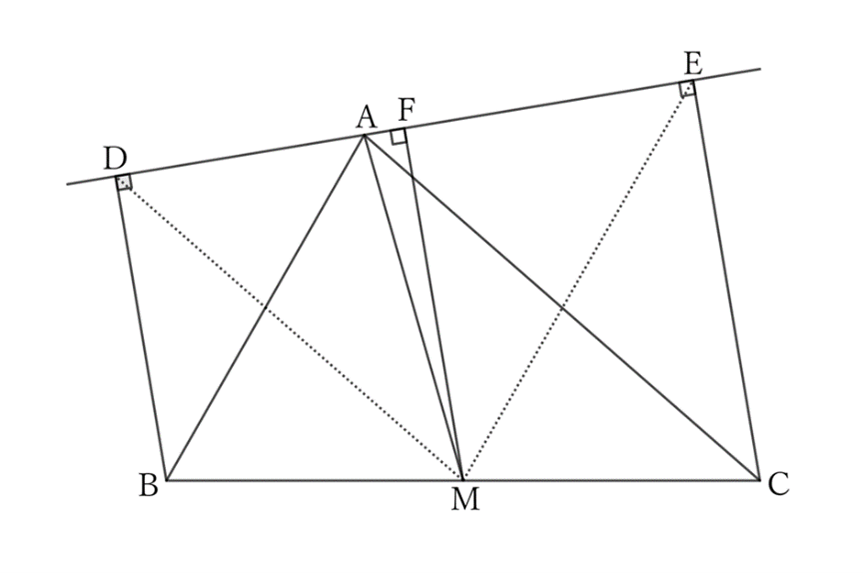
Let $F$ be the foot of the perpendicular line drawn from $M$ to $DE$. Then,
$$BD∥MF∥CE.$$
Since $M$ is the midpoint of $BC$,
$$DF=FE.$$
Therefore, $M$ lies on the perpendicular bisector of $DE$ and is the vertex of the isosceles triangle $MDE$.
$$∴ \ MD=ME.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.17