Problem
In a triangle $ABC$, let $∠C=2∠B$.
Then, if we draw a perpendicular line $AD$ from $A$ to $BC$, the difference between $DB$ and $DC$ is equal to $AC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
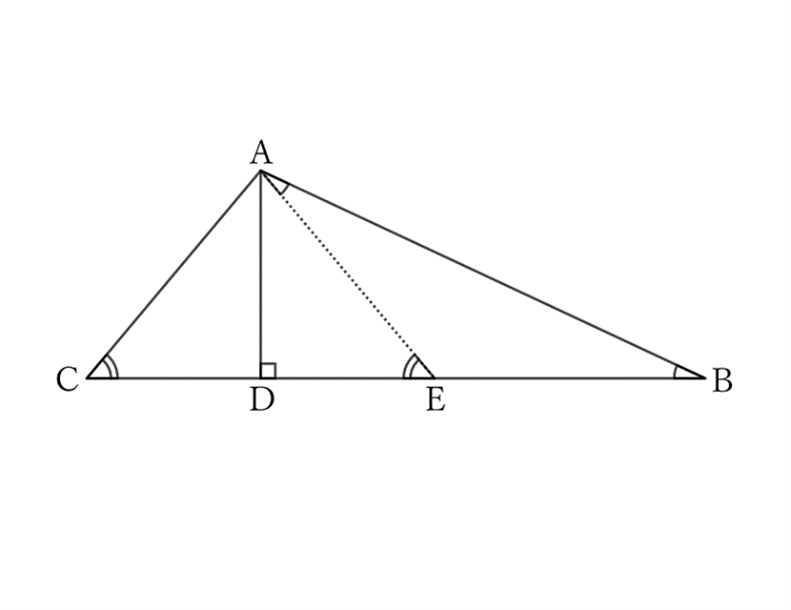
If we take a point $E$ on $DB$ where $DC=DE$, the triangle $ACE$ is an isosceles triangle with $A$ as the vertex. Thus,
$$AC=AE.$$
If $∠B=θ$, then from the problem statement,
$$∠C=2θ,$$
$$∴ \ ∠AEC=2θ.$$
$∠AEB$ is one angle of the triangle $AEB$. Since $∠AEC$ is an exterior angle of $∠AEB$,
$$∠BAE=θ.$$
Therefore, since the triangle $AEB$ is an isosceles triangle with $E$ as the vertex,
$$AE=EB.$$
Therefore,
$$AC=EB=DB-DE=DB-DC.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.17