Problem
If the feet of the perpendicular lines drawn from $A$ and $B$ to the opposite sides of a triangle $ABC$ are $D$ and $E$, respectively, and the midpoint of $AB$ is $F$, then
$$∠EDF=∠C.$$
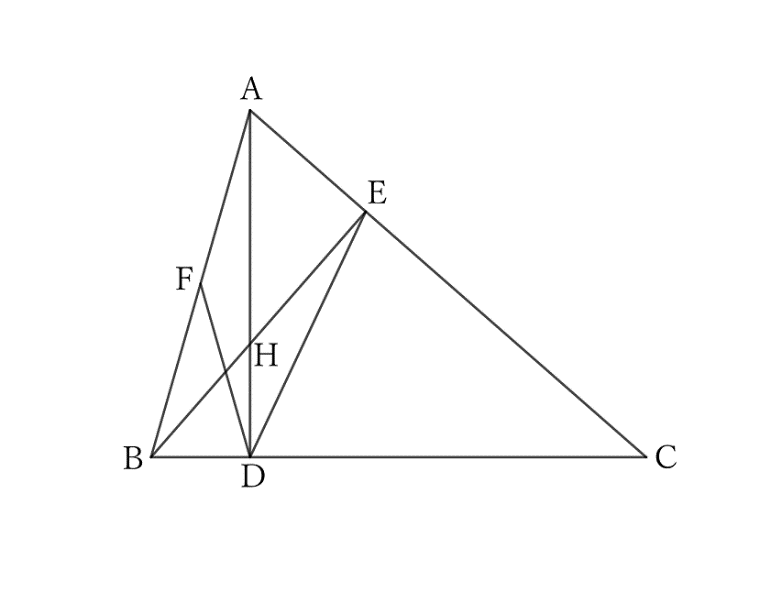
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
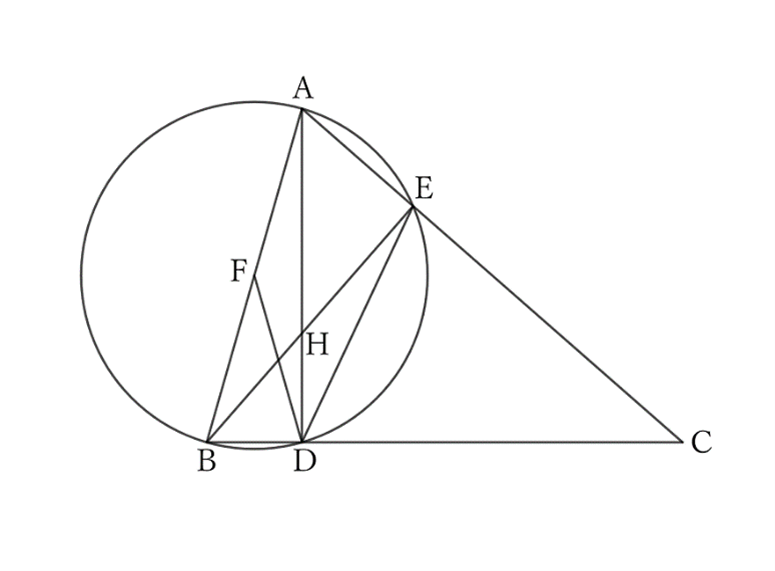
If the intersection of $AD$ and $BE$ is $H$, then $∠C$ and $∠EHD$ form supplementary angles to each other, and thus,
$$∠AHE=∠C,$$
$$∠AHE=∠HDE+∠HED,$$
$$∴ \ ∠C=∠HDE+∠HED.$$
Then, since $∠AEB=∠ADB=∠R$, $A$, $B$, $D$ and $E$ are on the same circumference, and
$$∠HED=∠FAD.$$
Since $F$ is the midpoint of the hypotenuse $AB$ of the right triangle $ABD$,
$$∠FAD=∠FDA,$$
$$∴ \ ∠C=∠HDE+∠FDA=∠EDF.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.18