P
roblem
In a triangle $ABC$, if the intersection of the bisectors of $∠B$ and $∠C$ is $O$, then
$$∠BOC=90°+\frac{1}{2}∠A.$$
Also, if the intersection of the bisectors of the exterior angles at $B$ and $C$ is $O’$, then
$$∠BO’ C=90°-\frac{1}{2}∠A.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
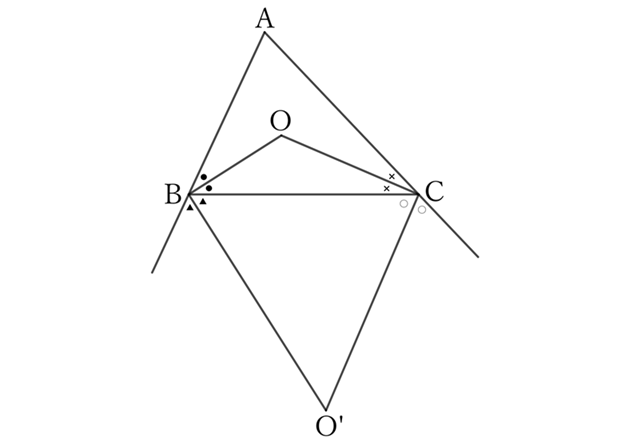
First, since the sum of the interior angles of a triangle is $180°$,
$$∠A+∠B+∠C=180°,$$
$$∴ \ ∠B+∠C=180°-∠A. \qquad [1]$$
$$∠BOC=180°-(∠OBC+∠OCB),$$
$$∴ \ ∠BOC=180°-\frac{1}{2} (∠B+∠C). \qquad [2]$$
Substituting $[1]$ for $[2]$, we have
$$∠BOC=180°-\frac{1}{2} (180°-∠A),$$
$$∴ \ ∠BOC=90°+\frac{1}{2}∠A. \qquad [3]$$
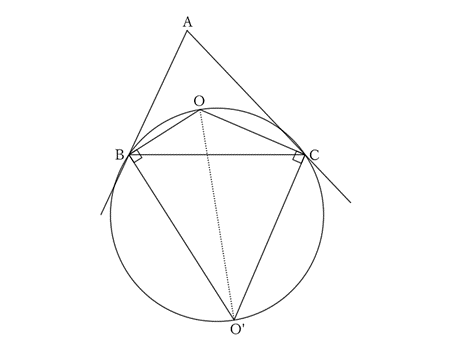
Next, since $∠OBO’=∠R=∠OCO’$, each vertex of quadrilateral $OBO’ C$ is inscribed in a circle of which diameter is $OO’$.
$$∠OBO’+∠OCO’=180°,$$
$$∴ \ ∠BOC+∠BO’ C=180°. \qquad [4]$$
Substituting $[3]$ into $[4]$, we have
$$90°+\frac{1}{2}∠A+∠BO’ C=180°,$$
$$∴ \ ∠BO’ C=90°-\frac{1}{2} ∠A.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.19