Problem
First, create a new triangle $A’B’C’$ by connecting the intersections of the bisectors of each exterior angle of the original triangle $ABC$.
Next, create a triangle $A^”B^”C^”$ by connecting the intersections of the bisectors of each exterior angle of the triangle $A’B’C’$.
If you create new triangles one after another in this way, the limit will be an equilateral triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
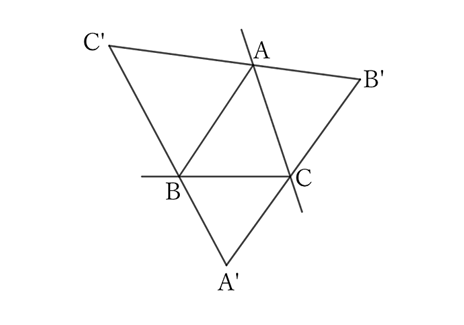
Regarding the triangle $A’B’C’$, from the problem $0079$,
$$∠A’=90°-\frac{1}{2}∠A,$$
$$∠B’=90°-\frac{1}{2}∠B,$$
$$∴ \ |∠A’-∠B’ |=\frac{1}{2} |∠A-∠B|.$$
Similarly, regarding the triangle $A^”B^”C^”$,
$$∠A^”=90°-\frac{1}{2}∠A’,$$
$$∠B^”=90°-\frac{1}{2}∠B’,$$
$$∴ \ |∠A^”-∠B^”|=\frac{1}{2} |∠A’-∠B’ |=\frac{1}{4} |∠A-∠B|.$$
Therefore, regarding the $n$-th triangle $A_n B_n C_n,$
$$|∠A_n-∠B_n |=\frac{1}{2^n} |∠A-∠B|.$$
In other words, the larger $n$ becomes, the smaller $|∠A_n-∠B_n |$,
$$∴ \displaystyle \lim_{n \to \infty} |∠A_n-∠B_n |=0.$$
Similarly, for $∠B_n$ and $∠C_n$,
$$\displaystyle \lim_{n \to \infty} |∠B_n-∠C_n |=0.$$
Therefore, when $n⟶∞$,
$$∠A_n=∠B_n=∠C_n.$$
Then, the triangle $A_n B_n C_n$ is an equilateral triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.19-20