Problem
Take any point $D$ on the side $AB$ of $△ABC$, and any point $F$ on the extension of $AC$.
Connecting $D$ and $F$, let $N$ be the intersection of the bisectors of $∠ADF$ and $∠ABC$, and let $M$ be the intersection of the bisectors of $∠AFD$ and $∠ACB$. Then,
$$∠BND=∠CMF.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
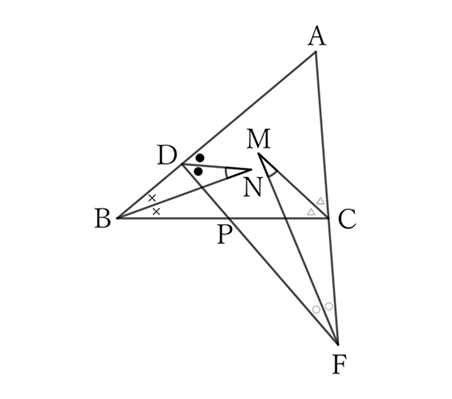
Since $N$ is an excenter of $△DPB$, from the problem $0077$,
$$∠BND=\frac{1}{2}∠DPB.$$
Similarly, since $M$ is an excenter of $△FCP$,
$$∠CMF=\frac{1}{2}∠FCP.$$
Since $∠DPB=∠FCP$,
$$∠BND=∠CMF.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.21