Problem
If we take any point $P$ on the bisector of the exterior angle of $∠A$ of $△ABC$, we get $$PB+PC>AB+AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
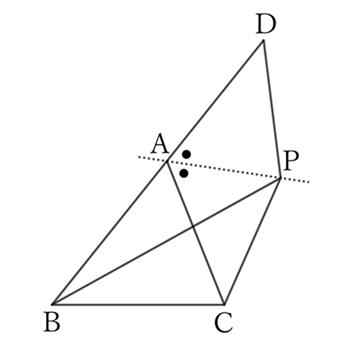
Take the point $D$ on the extension of $BA$ so that $AC=AD$.
Then, $△ACP$ and $△ADP$ share the side $AP$,
$$AC=AD \qquad and \qquad ∠CAP=∠DAP,$$
$$∴ \ △ACP≡△ADP,$$
$$∴ \ PC=PD.$$
Regarding $△BDP$,
$$PB+PD>BD,$$
$$∴ \ PB+PC>BD.$$
However, since $BD=AB+AC$,
$$PB+PC>AB+AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.21