Problem
Let $E$ and $F$ be the feet of the perpendiculars drawn from both ends $B$ and $C$ of the base to the bisector of the apex angle $∠A$ of $△ABC$, and let $G$ be the midpoint of $BC$.
Then, $△GEF$ is an isosceles triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
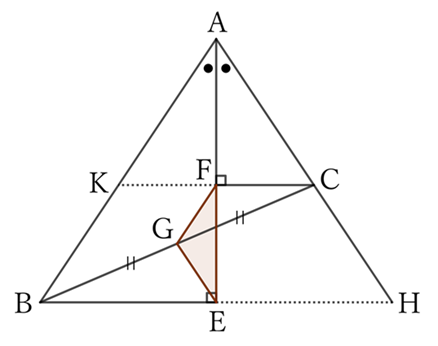
Let $H$ be the intersection of the extensions of $BE$ and $AC$, and let $K$ be the intersection of the extension of $CF$ and the side $AB$.
Then, $△ABE$ and $△AHE$ share the side $AE$,
$$∠BAE=∠HAE \qquad and \qquad ∠AEB=∠AEH \ (=∠R),$$
$$∴ \ △ABE≡△AHE,$$
$$∴ \ BE=HE.$$
Similarly, $△ACF$ and $△AKF$ share the side $AF$,
$$∠CAF=∠KAF \qquad and \qquad ∠AFC=∠AFK \ (=∠R),$$
$$∴ \ △ACF≡△AKF,$$
$$∴ \ CF=KF.$$
$△ABH$ is an isosceles triangle and $BH∥KC$. Therefore,
$$CH=BK. \qquad [1]$$
Regarding $△BCH$ and $△BGE$,
$$BG=\frac{1}{2} BC, \quad BE=\frac{1}{2} BH, \quad and \quad ∠GBE=∠CBH,$$
$$∴ \ △BCH〜△BGE,$$
$$∴ \ GE=\frac{1}{2} CH. \qquad [2]$$
Regarding $△CBK$ and $△CGF$,
$$CG=\frac{1}{2} CB, \quad CF=\frac{1}{2} CK, \quad and \quad ∠BCK=∠GCF,$$
$$∴ \ △CBK〜△CGF,$$
$$∴ \ GF=\frac{1}{2} BK. \qquad [3]$$
From $[1], \ [2]$ and $[3]$,
$$GE=GF.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.22