Problem
In $△ABC$, if we draw perpendiculars $BG$ and $CH$ from $B$ and $C$ to the bisector of the exterior angle of $∠A$, and let $AD$ be the bisector of $∠A$, then $CG, \ BH$ and $AD$ pass through the same point.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
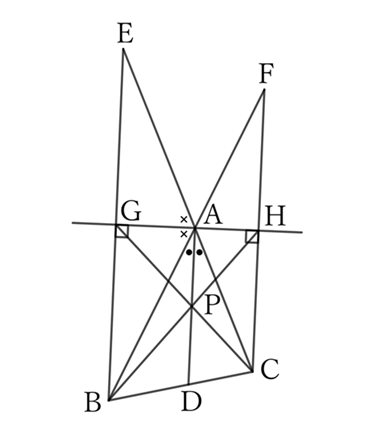
Let $E$ be the intersection of the extensions of $BG$ and $CA$, and $F$ be the intersection of the extensions of $CH$ and $BA$.
Since $AG$ is the bisector of $∠EAB$ and $AG⊥EB$, $G$ is the midpoint of $EB$.
From the figure, since $∠GAD=∠R$ and $AG⊥EB,$
$$EB∥AD.$$
Therefore, if the intersection of $CG$ and $AD$ is $P$, then
$$EG∶AP=GB∶PD,$$
$$∴ \ AP×GB=PD×EG,$$
$$∴ \ AP=PD. \qquad (∵ \ EG=GB)$$
That is, $P$ is the midpoint of $AD$, and $CG$ passes through the midpoint of $AD$.
Similarly, $BH$ also passes through the midpoint of $AD$.
Therefore, $CG, \ BH$ and $AD$ pass through the same point.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.22