Problem
Let $D$ and $E$ be the feet of the perpendiculars drawn from $C$ to the bisectors of $∠A$ of $△ABC$ and its exterior angle, respectively, and let $M$ be the midpoint of the side $BC$. Then, $M, \ D$ and $E$ are on the same straight line.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
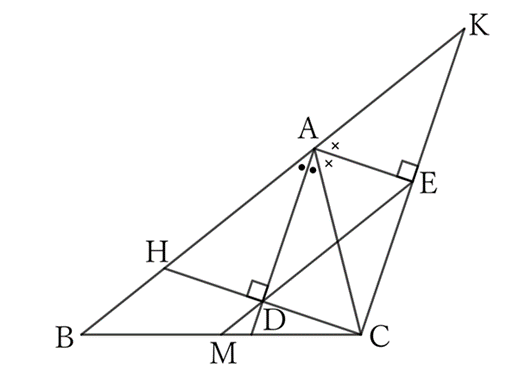
Let $H$ be the intersection of the extension of $CD$ and $AB$, and $K$ be the intersection of the extensions of $CE$ and $BA$.
Then, from $△ACD≡△AHD$, $D$ is the midpoint of $CH$, and from $△ACE≡△AKE$, $E$ is the midpoint of $CK$.
Therefore, the midpoints $M, \ D$ and $E$ of $CB, \ CH$ and $CK$ are on a straight line parallel to $KB$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.22-23