Problem
In $△ABC$, if $∠B=60°$ and the points where the bisectors of $∠A$ and $∠C$ intersect with $BC$ and $AB$ are $D$ and $E$, respectively,
$$CD+AE=AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
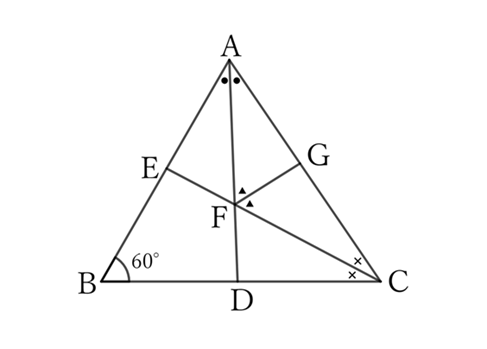
Let $F$ be the intersection of $AD$ and $CE$, and let $FG$ be the bisector of $∠AFC$.
Since $∠B=60°$,
$$∠A+∠C=120°,$$
$$∴ \ ∠FAC+∠FCA=60°,$$
$$∴ \ ∠AFC=120°,$$
$$∴ \ ∠AFG=∠CFG=60°,$$
$$∴ \ ∠AFE=∠CFD=60°.$$
$△CDF$ and $△CGF$ share the side $CF$,
$$∠FCG=∠FCD \qquad and \qquad ∠CFG=∠CFD \ (=60°),$$
$$∴ △CDF≡△CGF,$$
$$∴ \ CD=CG. \qquad [1]$$
$△AEF$ and $△AGF$ share the side $AF$,
$$∠FAE=∠FAG \qquad and \qquad ∠AFE=∠AFG \ (=60°),$$
$$∴ \ △AEF≡△AGF,$$
$$∴ \ AE=AG. \qquad [2]$$
However,
$$CG+AG=AC.$$
Thus, from $[1]$ and $[2]$,
$$CD+AE=AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.23