Problem
In $△ABC$, suppose $AB>AC$. Then, if we draw the median line $AD$,
$$∠BAD<∠CAD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
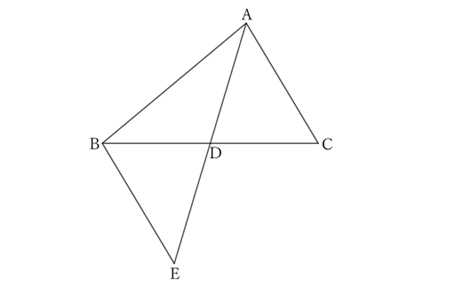
Let $E$ be the intersection point of the line parallel to $AC$ that passes through $B$ and the extension of $AD$.
Then, since $BD=CD, \ ∠ADC=∠EDB$, and $AC∥BE$,
$$∠ACD=∠EBD,$$
$$∴ \ △ACD≡△EBD,$$
$$∴ \ AC=EB \qquad and \qquad ∠CAD=∠BED.$$
Regarding $△ABE,$
$$AB>EB,$$
$$∴ \ ∠BAE<∠BEA,$$
$$∴ \ ∠BAD<∠BED,$$
$$∴ \ ∠BAD<∠CAD.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.24.