Problem
The medians of the three sides of a triangle intersect at a point located $\frac{2}{3}$ of the way from each vertex.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
Let the three medians of $△ABC$ be $AM, \ BD$ and $CE$ respectively.
Let $G$ be the intersection of $AM$ and $BD$, and $F$ be the intersection of the extension of $AM$ with the line passing through $B$ and parallel to $EG$.
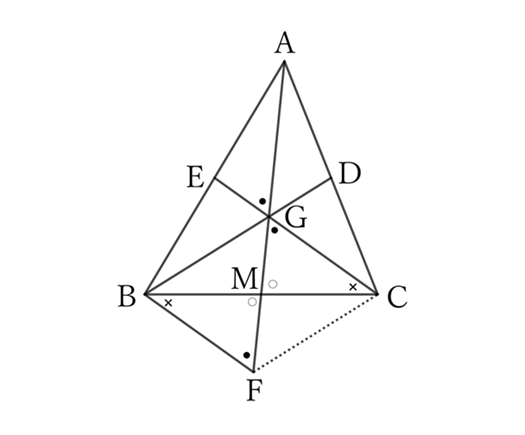
$△ABF$ and $△AEG$ share $∠BAF \ (=∠EAG)$, and since $BF∥EG$,
$$∠AFB=∠AGE,$$
$$∴ \ △ABF \sim △AEG.$$
Since $AB∶AE=2∶1$,
$$AF∶AG=2∶1,$$
$$∴ \ AG=GF.$$
Regarding $△MBF$ and $△MCG$,
$$MB=MC, \qquad ∠MBF=∠MCG, \qquad and \qquad ∠BMF=∠CMG,$$
$$∴ \ △MBF=△MCG,$$
$$∴ \ MG=MF,$$
$$∴ \ AG∶MG=2∶1.$$
Let $P$ be the intersection of $AM$ and $CE$, and $H$ be the intersection of the extension of $AM$ and a line passing through $C$ and parallel to $DP$.
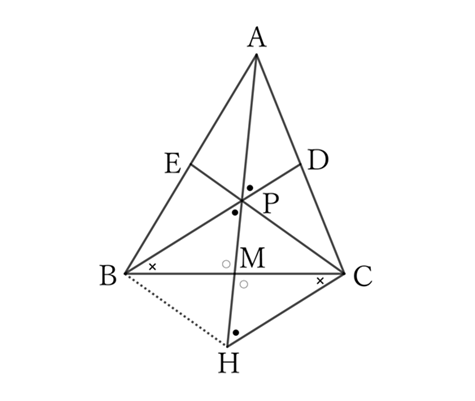
$△ACH$ and $△ADP$ share $∠CAH \ (=∠DAP)$, and since $CH∥DP$,
$$∠AHC=∠APD,$$
$$∴ \ △ACH \sim △ADP.$$
Since $AC∶AD=2∶1$,
$$AH∶AP=2∶1,$$
$$∴ \ AP=HP.$$
For $△MBP$ and $△MCH$,
$$MB=MC, \qquad ∠MBP=∠MCH, \qquad and \qquad ∠BMP=∠CMH,$$
$$∴ \ △MBP=△MCH,$$
$$∴ \ MP=MH,$$
$$∴ \ AP∶MP=2∶1.$$
Since both $G$ and $P$ are points that divide $AM$ into $2∶1$,
$$G=P.$$
Similarly,
$$BG∶DG=2∶1 \qquad and \qquad CG∶EG=2∶1.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.25.