Problem
In $△ABC$, let the two medians be $BE$ and $CF$. If $AB>AC$, then
$$BE>CF.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
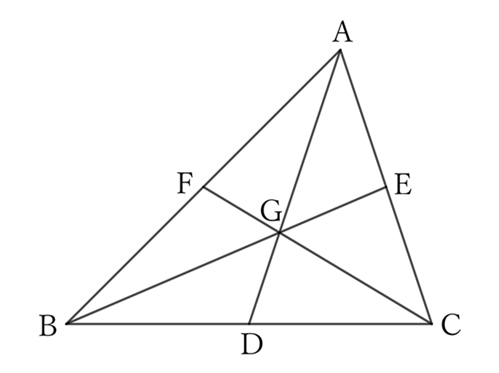
Let the other median be $AD$, and the center of gravity of $△ABC$ be $G$.
$△ABD$ and $△ACD$ share the side $AD$,
$$BD=CD \qquad and \qquad AB>AC,$$
$$∴ \ ∠ADB>∠ADC.$$
$△GBD$ and $△GCD$ share the side $GD$,
$$BD=CD \qquad and \qquad ∠GDB>∠GDC,$$
$$∴ \ BG<CG.$$
However,
$$BE=\frac{3}{2} BG \qquad and \qquad CF=\frac{3}{2} CG,$$
$$∴ \ BE<CF.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.25.