Problem
Take the points $E$ and $F$ on the sides $AB$ and $AC$ of $△ABC$ respectively, and $BE$ and $CF$ intersect at $G$.
If $2GE=GB$ and $2GF=GC$, then $G$ is the center of gravity of $△ABC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
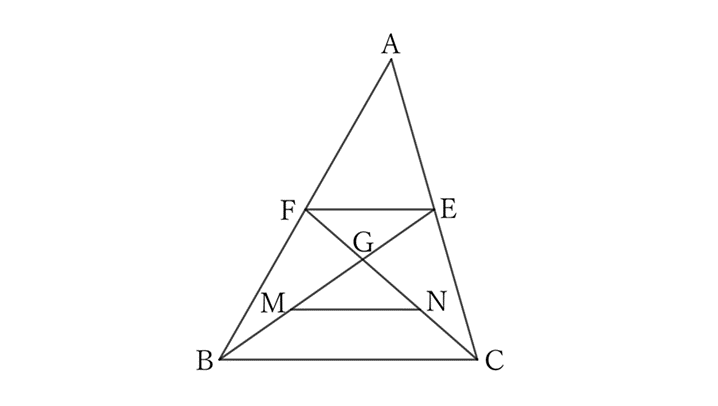
If the midpoints of $BG$ and $CG$ are $M$ and $N$ respectively,
$$BC∥MN \qquad and \qquad MN=\frac{1}{2} BC.$$
Regarding $△GEF$ and $△GMN$,
$$∠EGF=∠MGN, \qquad GE=GM, \qquad and \qquad GF=GN,$$
$$∴ \ △GEF≡△GMN,$$
$$∴ \ EF=MN \ (=\frac{1}{2} BC).$$
From $△GEF≡△GMN$,
$$∠GEF=GMN,$$
$$∴ \ EF∥MN,$$
$$∴ \ EF∥BC.$$
Therefore, $F$ and $E$ are the midpoints of $AB$ and $AC$ respectively, and $G$, the intersection of the medians $BE$ and $CF$, is the center of gravity of $△ABC$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.25.