Problem
The sum of the lengths of the perpendicular lines $AL, \ BM$, and $CN$ drawn from the vertices of $△ABC$ to a line outside the triangle is equal to three times the length of the perpendicular line $GP$ drawn from the center of gravity $G$ of the triangle to the line outside the triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
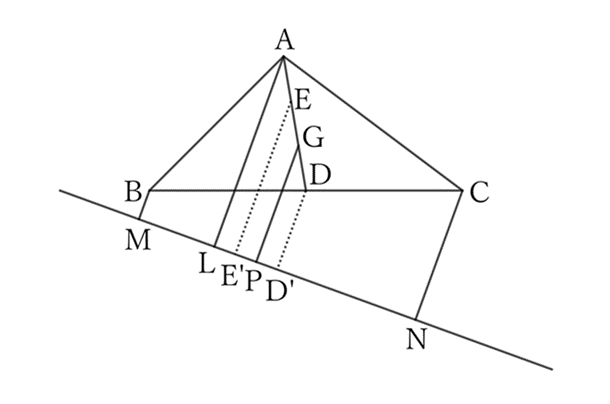
If the feet of the perpendicular lines drawn from the midpoint $D$ of $BC$ and the midpoint $E$ of $AG$ are $D’$ and $E’$, respectively, then
$$AL+GP=2EE’. \qquad [1]$$
$$EE’+DD’=2GP. \qquad [2]$$
$$BM+CN=2DD’. \qquad [3]$$
From $[1]+[2]+[3]$,
$$AL+GP+EE’+DD’+BM+CN=2EE’+2GP+2DD’,$$
$$∴ \ AL+BM+CN+GP+(EE’+DD’ )=2GP+2(EE’+DD’ ),$$
$$∴ \ AL+BM+CN+GP+2GP=2GP+4GP,$$
$$∴ \ AL+BM+CN=3GP.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.25-26.