Problem
If the feet of perpendicular lines drawn from vertices $A, \ B$, and $C$ to any line $XY$ passing through the center of gravity $G$ of $△ABC$ are $P, \ Q$, and $R$ respectively, then
$$AP=BQ+CR.$$
However, $A$ is on the opposite side of $XY$ from $B$ and $C$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
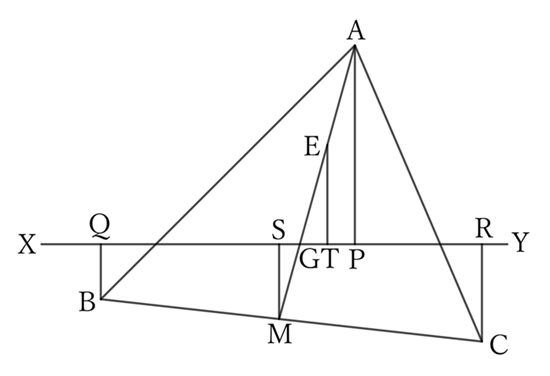
Let $M$ be the point where the extension of $AG$ intersects with $BC$, $E$ be the midpoint of $AG$, and let $S$ and $T$ be the feet of the perpendiculars drawn from $M$ and $E$ to the line $XY$.
Since $AM$ passes through the center of gravity $G$, it is the median,
$$AE=EG=GM,$$
$$∴ \ ET=MS=\frac{1}{2} AP.$$
Since $M$ is the midpoint of the side $BC$,
$$BM=MC,$$
$$∴ \ BQ+CR=2MS,$$
$$∴ \ AP=BQ+CR.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.26.