If the medians $BE$ and $CF$ of $△ABC$ are extended so that $BE=EG$ and $CF=FH$, then $G, \ A$ and $H$ are collinear.

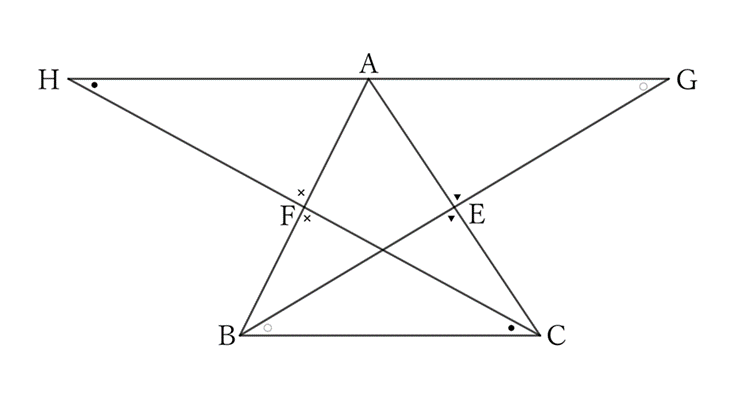
For $△AFH$ and $△BFC$,

$$∠AFH=∠BFC, \qquad AF=BF, \qquad and \qquad FH=FC,$$

$$∴ \ △AFH≡△BFC,$$

$$∴ \ ∠AHF=∠BCF,$$

$$∴ HA∥BC.$$

For $△AEG$ and $△CEB$,

$$∠AEG=∠CEB, \qquad AE=CE, \qquad and \qquad EG=EB,$$

$$∴ \ △AEG≡△CEB,$$

$$∴ \ ∠AGE=∠CBE,$$

$$∴ \ GA∥BC.$$

$HA$ and $GA$ share the point $A$ and are both parallel to $BC$.

Thus, $G, \ A$ and $H$ are collinear.