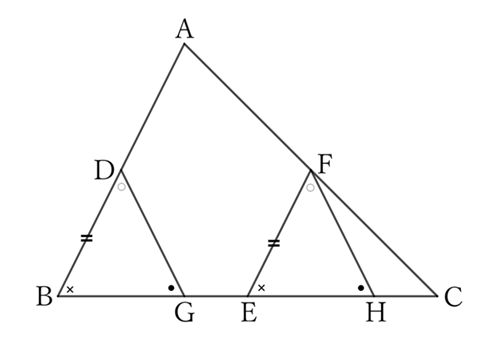
Let $D, \ E$ and $F$ be the midpoints of the sides $AB, \ BC$ and $CA$ of $△ABC$, respectively.

Draw parallel lines in any direction from $D$ and $F$, and let $G$ and $H$ be the points where they intersect with $BC$, respectively. Then,

$$BG=EH.$$

Since $DG∥FH$,

$$∠DGB=∠FHE. \qquad [1]$$

Since $△ABC$ and $△FEC$ share $∠C$, $AC∶FC=2∶1$ and $BC∶EC=2∶1$,

$$△ABC \sim △FEC,$$

$$∴ \ AB∶FE=2∶1,$$

$$∴ \ DB=FE. \qquad [2]$$

Since $AB∥FE$,

$$∠DBG=∠FEH. \qquad [3]$$

From $[1]$ and $[3]$,

$$∠BDG=∠EFH. \qquad [4]$$

From $[2], \ [3]$ and $[4]$,

$$△DBG≡△FEH,$$

$$∴ \ BG=EH.$$