Problem
Construct the median $AD$ of $△ABC$, and draw a line parallel to $AD$ from any point $P$ on the side $BC$.
Let $Q$ and $R$ be the points where the line intersects with $AB$ and $AC$, or their extensions.
Then, the length of $PQ+PR$ is constant regardless of the location of $P$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
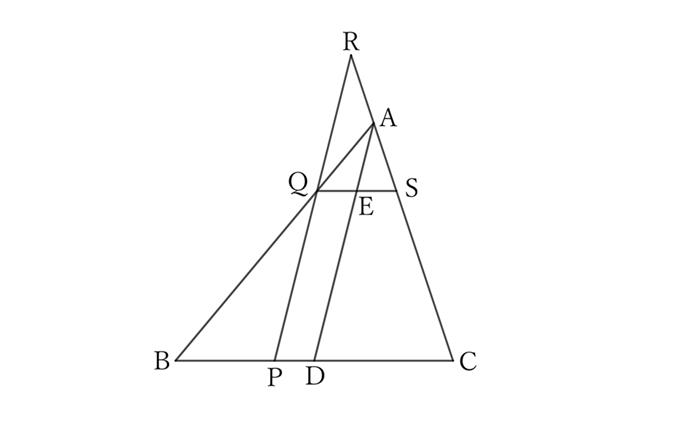
Draw a straight line parallel to $BC$ through $Q$, and let $E$ and $S$ be the points of intersection of this line with $AD$ and $AC$, respectively.
Since $△ABC \sim △AQS$ and $D$ is the midpoint of $BC$, $E$ is the midpoint of $QS$.
Since $△RQS \sim △AES$ and $E$ is the midpoint of $QS$,
$$RQ∶AE=2∶1.$$
Then,
$$AD=DE+AE \qquad and \qquad PR=PQ+RQ.$$
Since $AD∥PR, \ PQ=DE$ and $RQ=2AE$,
$$∴ \ PR=DE+2AE,$$
$$∴ \ PQ+PR=2PQ+RQ=2(DE+AE)=2AD.$$
In other words, no matter where $P$ is on $BC$, the length of $PQ+PR$ is always constant and twice the length of the median line $AD$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.27.