Problem
Two lines $x$ and $y$ intersect at point $O$.
On each of these lines are equal-length segments $AB$ and $CD$, and the midpoints of $AC$ and $BD$ are $M$ and $N$, respectively.
Then, the line $MN$ has a constant direction regardless of the positions of $AB$ and $CD$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
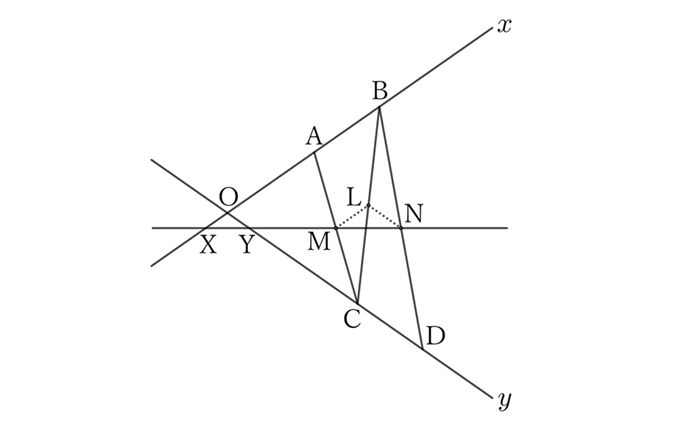
Let $L$ be the midpoint of $BC$, and $X$ and $Y$ be the points where the lines $x$ and $y$ intersect with the line $MN$, respectively.
$△CAB$ and $△CML$ share $∠ACB \ (=∠MCL)$,
$$CA∶CM=2∶1 \qquad and \qquad CB∶CL=2∶1,$$
$$∴ \ △CAB∼△CML,$$
$$∴ \ AB∶ML=2∶1 \qquad and \qquad AB∥ML.$$
Similarly, $△BCD$ and $△BLN$ share $∠CBD \ (=∠LBN)$,
$$BC∶BL=2∶1 \qquad and \qquad BD∶BN=2∶1,$$
$$∴ \ △BCD∼△BLN,$$
$$∴ \ CD∶LN=2∶1 \qquad and \qquad CD∥LN.$$
Since $AB=CD$,
$$ML=NL,$$
$$∴ \ ∠LMN=∠LNM.$$
For $△OXY$,
$$OX∥LM \qquad and \qquad OY∥LN,$$
$$∴ \ ∠OXY=∠LMN \qquad and \qquad ∠OYX=∠LNM,$$
$$∴ \ ∠OXY=∠OYX \qquad (∵ \ ∠LMN=∠LNM).$$
In other words, regardless of the positions of $AB$ and $CD$, the line $XY \ (=MN)$ is parallel to the bisector of the angle between the lines $x$ and $y$ and always in a constant direction.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.27.