Problem
How many lines are equidistant from the three vertices of $△ABC$ ?
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
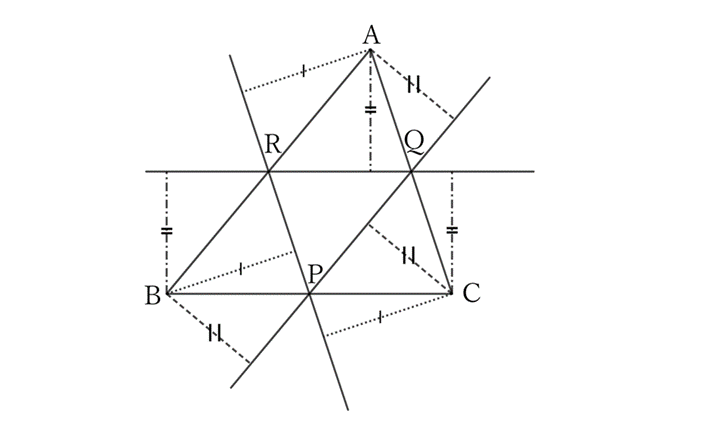
Let $P, \ Q$ and $R$ be the midpoints of $BC, \ CA$ and $AB$, respectively.
Every line through $R$ is equidistant from $A$ and $B$, and every line through $P$ is equidistant from $B$ and $C$.
Therefore, the line through $R$ and $P$ is equidistant from $A, \ B$ and $C$.
Similarly, the line through $P$ and $Q$, and the line through $Q$ and $R$ are equidistant from $A, \ B$ and $C$.
Thus, there are three lines that are equidistant from the three vertices of a triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.27-28.