Problem
If you drop a perpendicular line $AD$ from the right-angled vertex $A$ of a rectangular triangle $ABC$ to the side $BC$,
$$∠C=∠BAD \qquad and \qquad ∠B=∠CAD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
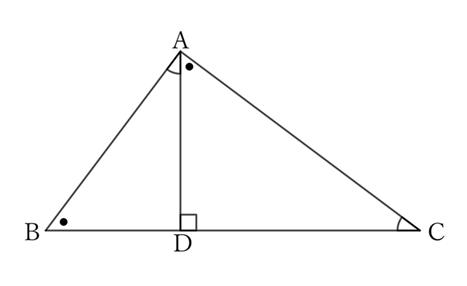
$△ABC$ and $△DBA$ share $∠B \ (=∠DBA)$, and
$$∠A=∠ADB=∠R.$$
$$∴ △ABC \sim △DBA,$$
$$∴ \ ∠C=∠BAD.$$
$△ABC$ and $△DAC$ share $∠C \ (=∠ACD)$, and
$$∠A=∠CDA=∠R.$$
$$∴ \ △ABC \sim △DAC,$$
$$∴ \ ∠B=∠CAD.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.28.