If $D$ is the intersection point of the bisector of the right-angled vertex $A$ of a rectangular triangle $ABC$ and the line that passes through the midpoint $M$ of the hypotenuse $BC$ and is perpendicular to $BC$, then

$$MA=MD.$$

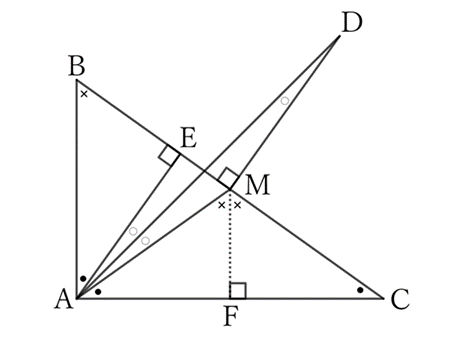
Let the feet of the perpendicular lines drawn from $A$ to $BC$ and from $M$ to $AC$ be $E$ and $F$, respectively.

Since $△MCF≡△MAF$,

$$∠MCF=∠MAF.$$

Since $△ABC \sim △FMC$,

$$∠BAC=∠MFC.$$

Since $△ABC \sim △EBA$,

$$∠BCA \ (=∠MCF) \ =∠BAE.$$

Since $∠BAD=∠CAD=45°$,

$$∠DAE=45°-∠BAE, \qquad ∠DAM=45°-∠MAF, \qquad and \qquad ∠MAF=∠BAE,$$

$$∴ \ ∠DAE=∠DAM.$$

Since $AE∥DM$,

$$∠DAE=∠ADM,$$

$$∴ \ ∠DAM=∠ADM.$$

Therefore, $△MAD$ is an isosceles triangle with $M$ as its vertex, and

$$MA=MD.$$