Problem
If $D$ is the foot of the perpendicular line drawn from the right-angled vertex $A$ of a rectangular triangle $ABC$ to the hypotenuse $BC$, then
$$AD+BC>AB+AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
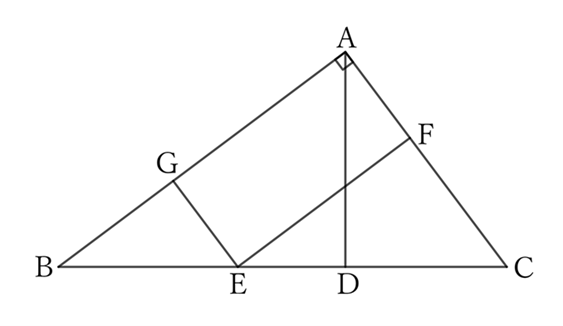
Take a point $E$ on the side $BC$ such that $AC=EC$, and let $F$ be the point where a line passing through $E$ and parallel to $AB$ intersects with $AC$.
Then, $△DAC$ and $△FEC$ share $∠DCA \ (=∠FCE)$,
$$∠ADC=∠EFC \ (=∠R) \qquad and \qquad AC=EC,$$
$$∴ \ △DAC≡△FEC,$$
$$∴ \ AD=EF \ (=GA).$$
For the right-angled triangle $GBE$, since $BE$ is the hypotenuse,
$$BE>GB.$$
Therefore,
$$AD+EC=GA+AC,$$
$$∴ \ AD+EC+BE>GA+GB+AC,$$
$$∴ \ AD+BC>AB+AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.29.