Take a point $D$ on the extension of the side $AB$ of a triangle $ABC$ such that $AB=BD$, and let $E$ be the point closest to $B$ of the two that divide $BC$ into thirds.

Then, if $AE=\frac{1}{3} CD$, $△ABC$ is a right triangle.

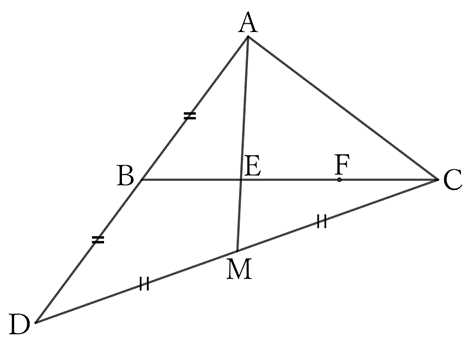
Regarding $△ACD$, $B$ is the midpoint of the side $AD$, and $E$ is the point that divides the median $CB$ into $2∶1$.

Thus, $E$ is the center of gravity of $△ACD$.

Therefore, $M$ is the midpoint of the side $CD$, and $E$ divides the median $AM$ into $2∶1$.

From the condition: $AE=\frac{1}{3} CD$,

$$AM=\frac{3}{2} AE=\frac{3}{2} × \frac{1}{3} CD=\frac{1}{2} CD,$$

$$∴ \ MA=MD=MC.$$

Since $△MAD$ is an isosceles triangle with $M$ as its vertex, $△ACD$ is a right triangle with $∠A=∠R$, and $△ABC$ is also a right triangle.