In a right triangle $ABC$,

$$∠A=∠R.$$
Let $D$ be the foot of the perpendicular line drawn from $A$ to $BC$, $E$ be the point where the bisector of $∠B$ intersects $AC$, $F$ be the foot of the perpendicular line drawn from $E$ to $BC$, and $G$ be the point of intersection of $AD$ and $BE$.

Then,
$(1)$ The quadrilateral $AEFG$ is a rhombus;
$(2)$ $△ABG$ and $△BDE$ have the same area.

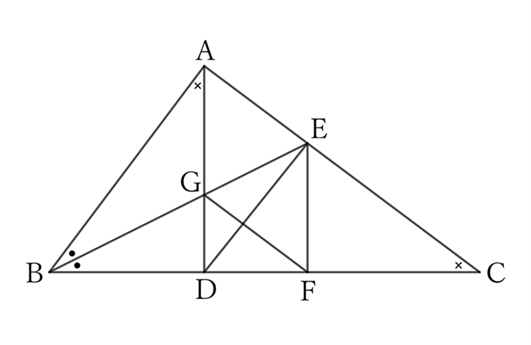
$(1)$ $△ABE$ and $△FBE$ share the side $BE$,
$$∠ABE=∠FBE \qquad and \qquad ∠EAB=∠EFB \ (=∠R),$$
$$∴ \ △ABE≡△FBE,$$
$$∴ \ AE=EF.$$
$△ABG$ and $△FBG$ share side $BG$,
$$∠ABG=∠FBG \qquad and \qquad AB=FB,$$
$$∴ \ △ABG≡△FBG,$$
$$∴ \ GA=FG.$$
Now, regarding $△AGE$,
$$∠AGE=∠ABG+∠BAG=∠EBC+∠C=∠AEG,$$
$$∴ GA=AE,$$
$$∴ \ AE=EF=FG=GA.$$
Therefore, the quadrilateral $AEFG$ is a rhombus.

$(2)$ If the areas of $△ABG$ and $△BDE$ are $S_1$ and $S_2$, respectively,
$$S_1=\frac{1}{2}×AG×BD \qquad and \qquad S_2=\frac{1}{2}×BD×EF.$$
From $(1)$,

$$AG=EF,$$
$$∴ \ S_1=S_2.$$